
Haibo Wu M. Sc.
Alumnus of the Pattern Recognition Lab of the Friedrich-Alexander-Universität Erlangen-Nürnberg
There is a critical need to reconstruct clinically usable images at a low dose. One way of achieving this is to reconstruct with as few projections as possible. The recently introduced compressed sensing (CS) theory uses sparsity as a prior and improves the reconstruction quality considerably using only few projections. CS assumes that medical images are sparse under certain sparsifying transform. Similar as iterative reconstruction method, CS formulates the reconstruction to an optimization problem with a additional L1 norm to promote the sparsity. Benefit from the sparsity, the error bound of CS is much smaller than traditional iterative approach. In this work, we introduce the sparsity level constaint as a prior to further decrease the error bound. We compared our algorithm against the traditional iterative reconstruction method and the total variation regularization method which is the state-of-art CS based reconstruction method. One numerical simulation and one invitro dataset were used for evaluation.
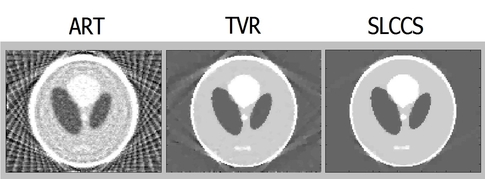
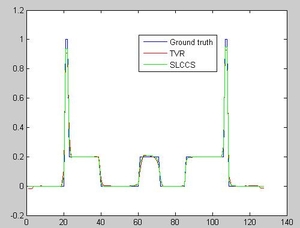
Fig. 1. Reconstruction resuts. Only 30 projections are used to perform the reconstruction. The left image is the reconstructed images and the right image plots the line profile of the center line of the image reconstructed by TVR and our SLCCS method.
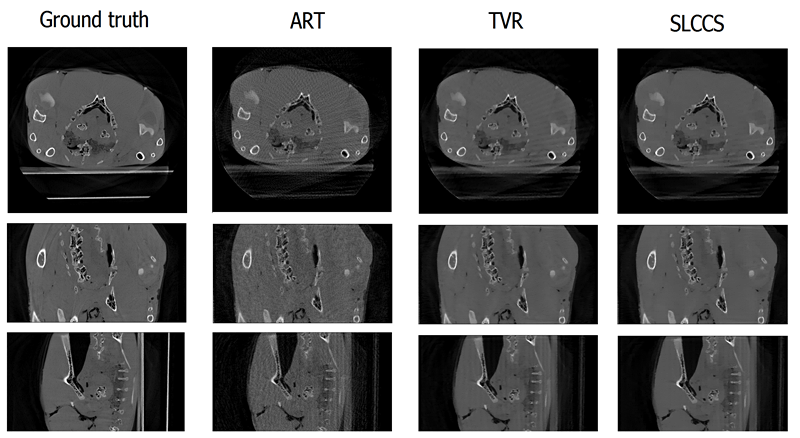
Fig.2. Reconstruction resuts of in vitro dataset. Only 100 projection images were used. The ground truth is the image reconstructed using FDK with the full projection images (496 projections).
Four dimensional computed tomography (4D-CT) is very important for treatment planning in thorax or abdomen area, e.g. for guiding radiation therapy planning. The respiratory motion makes the reconstruction problem ill-posed. Recently, compressed sensing theory was introduced. It uses sparsity as a prior to solve the problem and improves image quality considerably. However, the images at each phase are reconstructed individually. The correlations between neighboring phases are not considered in the reconstruction process. In this paper, we propose the spatial-temporal total variation regularization (STTVR) method which not only employs the sparsity in the spatial domain but also in the temporal domain. (See Fig. 1) The algorithm is validated with XCAT thorax phantom. The Euclidean norm of the reconstructed image and ground truth is calculated for evaluation. The results indicate that our method improves the reconstruction quality by more than 50% compared to standard ART[1] (see Table 1 and Fig. 2).
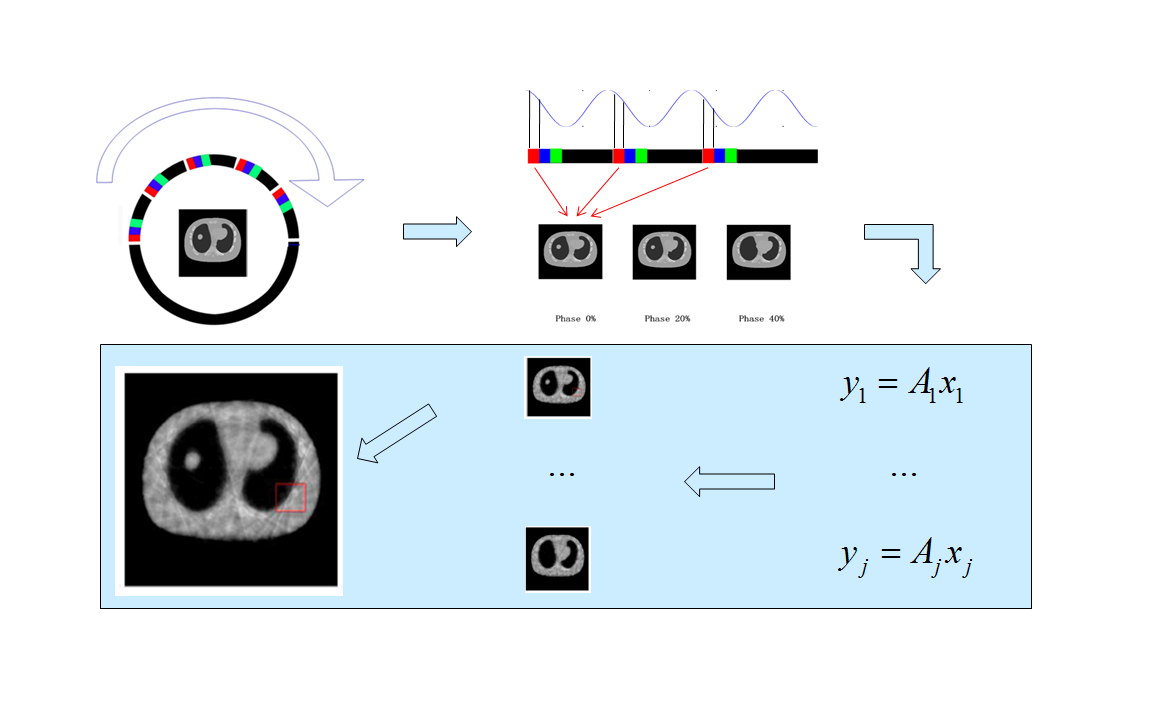
Fig. 1. Reconstruction process.
![Fig. 2. Reconstruction results. The first row shows the image of phase 0 and the second row shows the image of phase 7. The firrst column is the ground truth. The second to the fourth column list the results reconstructed by standard ART, TVR[2] and our method. Only 20 iterations are used for all the method. Fig. 2. Reconstruction results. The first row shows the image of phase 0 and the second row shows the image of phase 7. The firrst column is the ground truth. The second to the fourth column list the results reconstructed by standard ART, TVR[2] and our method. Only 20 iterations are used for all the method.](https://www5.cs.fau.de/fileadmin/Persons/WuHaibo/RESULTS.png)
Fig. 2. Reconstruction results. The first row shows the image of phase 0 and the second row shows the image of phase 7. The firrst column is the ground truth. The second to the fourth column list the results reconstructed by standard ART, TVR[2] and our method. Only 20 iterations are used for all the method.
Table 1. Euclidean norm of the reconstruction results and the ground truth.&nb
| ART | TVR | STTVR | |
|---|---|---|---|
| Phase 0 | 954.129 | 528.115 | 341.590 |
| Phase 7 | 891.567 | 501.844 | 334.336 |
Mean of all 15 phases | 922.938 | 517.378 | 346.189 |
Learn more: ![]() Spatial-temporal Total Variation Regularization (STTVR) for 4D-CT Reconstruction
Spatial-temporal Total Variation Regularization (STTVR) for 4D-CT Reconstruction
[1] G. L. Zeng, Medical Image Reconstruction, High Education Press, China, 2009.
[2] E. Y. Sidky and X. Pan, Image reconstruction in circular cone-beam computed tomography by constrained total-variation minimization, Phys. Med. Bio. 53, pp. 4777-4807, 2008.
4D-CT is an important tool for treatment simulation and treatment planning in radiotherapy. However,
- Due to motion, only few projections can be used to reconstruct the image of a certain respiratory phase.
- Lack of projections degrades reconstruction quality.
We propose a novel method based on iterative hard thresholding and compressed sensing. The prior knowledge from both methods are integrated into our reconstruction problem formulation. In the experiments, we validate our method with XCAT phantom data. The Euclidean norm of the reconstructed images and the ground truth are calculated for quantitative evaluation. We also compared our SLCCS algoritm against four state-of-art methods, namely,
- ART (simultaneous Algebraic Reconstruction Technique) [1]
- TVR (Total Variation Regularization ) [2]
- WR (Wavelet Regularition) [3]
- IHT (Iterative Hard thresholding) [4].
The results show that our method outperforms the traditional reconstruction method. (see Fig. 1 and Table I)
Compressed sensing based CT reconstruction
Computed tomography (CT) is considered as a radiation-intensive procedure, yet it becomes more and more common. The risk of radiation induced disease makes a strong need to reconstruct computed tomography (CT) images with practically useful quality using as low radiation as possible[1]. One strategy is to use limited number of projections. To reduce the radiation dose, the projection images are only acquired at few views. The major challenging is that the number of observation is much less than the number of unknowns. Recently, Candes, Romberg and Tao proposed a new mathematical theory, compressed sensing(CS), which can perform nearly exact image reconstruction with only few measurements[3]. Based on this theory, we aim to develop a CT reconstruction method requiring as few projection images as possible. According to the framework of compressed sensing, the image should firstly be sparsifying and then be reconstructed by a constrained l1 norm minimization method. We used total variation as the sparsifying transform and tested the algorithm using Shepp-Logan phantom. The reconstructed image is almost the same with the original image with only 20 projection images[Fig. 1].
Fig. 1 Reconstructed results
Reference
[1] Cho, S., Sidky, E. Y., Bian, J., Pelizzari, C. A., & Pan, X. (2008). A preliminary investigation of using prior information for potentially improving image reconstruction in few-view CT. in Medical Imaging, vol. 6913 of Proc. SPIE.
[2] Candes, E., Romberg, J., & Tao, T. (2006). Robust Uncertainty Principles : Exact Signal Reconstruction from Highly Incomplete Frequency Information. Foundations of Computational Mathematics, 6(2), 227-254.




