Organ segmentation is frequently performed in clinical routine, for example prior to an organ transplantation.

Since soft tissue contrast is often low in computed tomography (CT) acquisitions, segmenting organs using only image information is often prone to fail. We therefore incorporate shape knowledge via a statistical shape model into the segmentation process in order to increase robustness.

Statistical Shape Model

One common approach is to incorporate shape knowledge through an active shape model (ASM) [1]. In this context, a shape is represented through a vector of landmark points. In order to obtain a statistical model, principal component analysis (PCA) is performed on a set of point vectors. This, however, requires the establishment of point correspondences across the training set, which often is a difficult task. We have instead chosen an implicit shape representation through signed distance maps, which does not require landmark points or point correspondences. The principle is illustrated through Fig. 1. PCA is then performed in a similar way on a set of signed distance maps.

Fig. 1. Explicit shape representation through landmark points (left) and implicit representation through signed distance map (right).

Boundary Appearance Model

Simple edge detectors using local differences are not reliable enough when segmenting organs from CT images. We therefore build a boundary appearance model by sampling intensity profiles from the known organ boundary during a training step. Traditionally, normal distributions of profile vectors were assumed. The appearance model is then given by the mean profile vector and the covariance matrix. In order to capture arbitrary distributions of profile vectors, we have integrated a nearest neighbor appearance model [2]. During the training step, false profile vectors are also sampled, with an offset from the true organ boundary, as illustrated through Fig. 2.

The boundary appearance model is integrated into a level set geodesic active contour. For each point part of the narrow band around the contour, a profile vector is sampled. Give the profile vector, a probability is estimated of the point belonging to the organ boundary. The active contour is then moved towards the most probable boundary points.

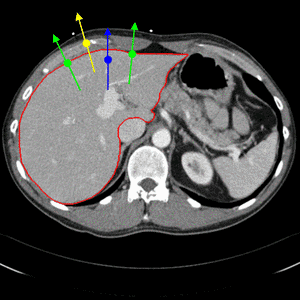
Fig. 2. Nearest neighbor boundary appearance model. Both true boundary profiles (green) as well as false boundary profiles with an offset (yellow and blue) are sampled during training.

Combined Active Contour and Shape Model

In order to integrate the statistical shape model into the segmentation process, we follow the approach of [3]. An energy functional measures the squared difference between active contour level set function and shape model level set function. The functional is optimized with respect to the contour, which yields an additional shape term for the level set equation. In the functional is also optimized with respect to the parameters of an affine transformation, which aligns the shape model with the active contour in the image. Furthermore, the functional is optimized with respect to the weights of the Eigen modes used for the shape model.

The evolution of the resulting implicit active shape model is show in Fig. 3.

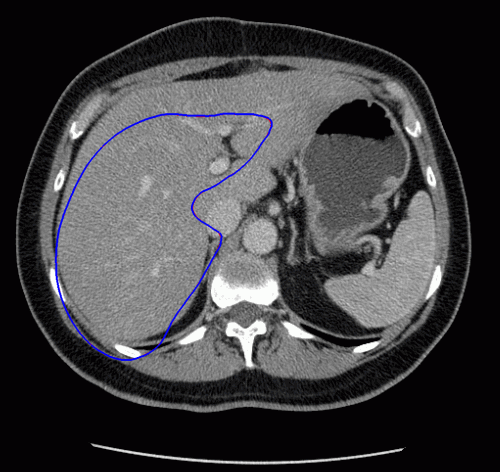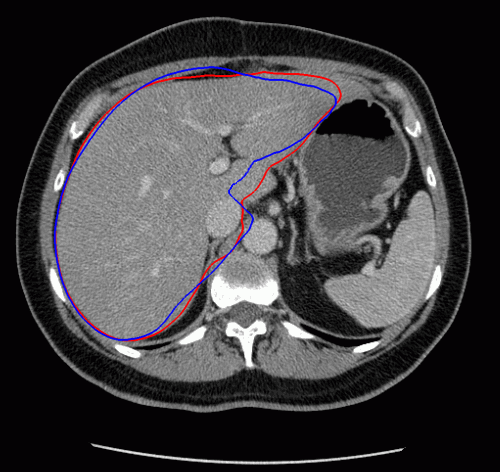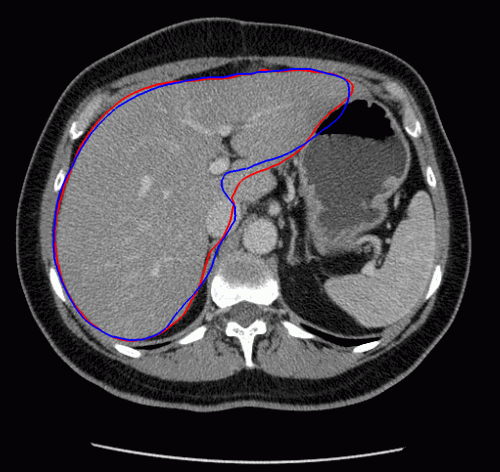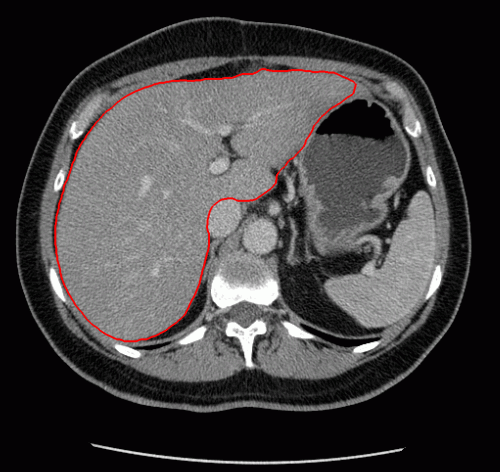
Fig. 3. Evolution of the implicit active shape model. The active contour is shown in red, the shape model in blue.

[1] T. F. Cootes, D. Cooper, C. J. Taylor, J. Graham, Active Shape Models – Their Training and Application. CVIU, 61(1):38-59, 1995

[2] B. van Ginnecken, A. F. Frangi, J. J. Staal, B. M. ter Haar Romeny, M. A. Viergever. Active Shape Model Segmentation with Optimal Features. IEEE Transactions on Med. Imaging, 21(8):924-933, 2002

[3] M. Rousson, N. Paragios, R. Deriche. Implicit Active Shape Models for 3D Segmentation in MR Imaging. MICCAI 2004, 3216:209-216, 2004