Image Denoising Algorithms Archive
What is the Image Denoising Algorithms Archive (IDAA)?
This webpage contains a collection of commonly used and state-of-the-art denoising algorithms. The algorithms were implemented, used, and testet at the pattern recognition lab. We intend to let this archive grow over time. In addition, the evaluation data we use for our journal paper publications can be downloaded, to facilitate reproducible research. For every algorithm and dataset, the references to the original and our publications are given, as well as the implementation author.
This website was originally created out of the Projekt  OCT Image Denoising, and we plan to compare several of the algorithms shown here for the purpose of denoising OCT images in an upcoming publication. However, the archive is intended to be useful for multiple purposes and various modalities.
OCT Image Denoising, and we plan to compare several of the algorithms shown here for the purpose of denoising OCT images in an upcoming publication. However, the archive is intended to be useful for multiple purposes and various modalities.
If you have a code that you want to add to the archive, please contact  Markus Mayer.
Markus Mayer.
You may use the code as you want. If this collection is helpful to your research, we would be grateful if you visit the homepage of the code author and search for articles that you find worth citing in your next article.
We do not give any guarantees for the correctnes of the codes.
Denoising Algorithms Matlab Code
The denoising methods below are implemented in Matlab (Mathworks, Inc.). The parameter exchange follows a common principle in all the codes, to ease the implementation of high quality quantitative evaluations.
| Method, Download | Image Examples | Reference | Description, Implementation Author |
|---|---|---|---|
| Calling examples (idaa_homepage.m) | 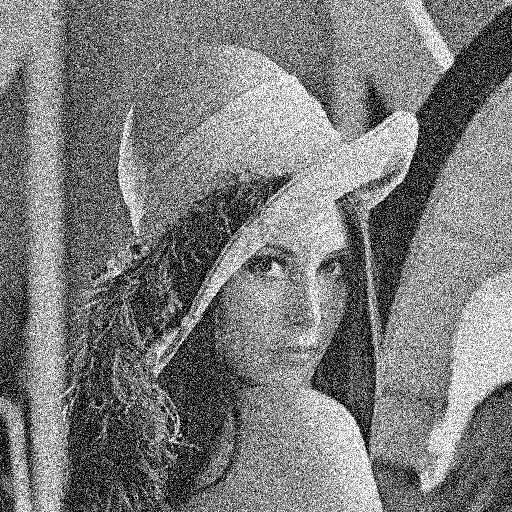 Original image: The famous "Lena" image, corrupted with noise. The image was scaled to a [0;1] intensity range and gaussian noise with a standard deviation of 0.2 added.
Original image: The famous "Lena" image, corrupted with noise. The image was scaled to a [0;1] intensity range and gaussian noise with a standard deviation of 0.2 added.
|
- | An example on how to call the various denoising algorithms. The example images shown in this table were created by this script.
Implementation author:  Markus Mayer Markus Mayer |
| Wavelet Thresholding (waveletHardThreshold.m, waveletSoftThreshold.m) |  Wavelet soft thresholding with the double densitiy dual tree wavelet and a threshold of 0.15.
Wavelet soft thresholding with the double densitiy dual tree wavelet and a threshold of 0.15.
|
Your favorite wavelet theory book may hold up as a reference for this technique. For the usage of the double density dual-tree complex wavelet transformation refer to: Ivan W. Selesnick: "The Double-Density Dual-Tree DWT", IEEE Transaction on Signal Processing, Vol. 52, No. 5, 2004 | Supports wavelet hard/soft thresholding. Wavelet may be the ones in the Matlab Wavelet toolbox. In addition, you can download the dual-tree and double densitiy dual-tree wavelet from Ivan Selesnick et al. (taco.poly.edu/WaveletSoftware).
Implementation author:  Markus Mayer Markus Mayer |
| Isotropic Diffusion (diffusionPeronaMalik.m) | 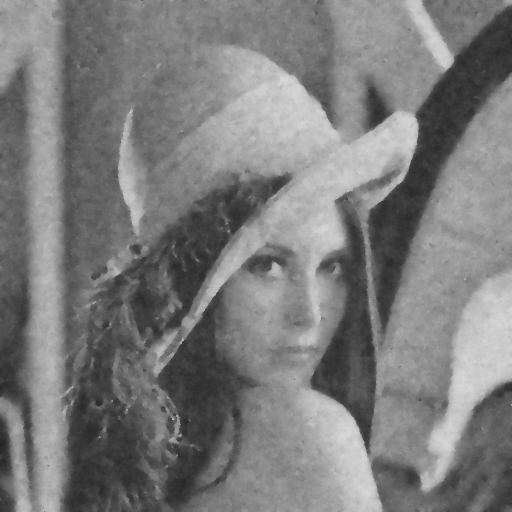 Complex diffusion with a sigma of 0.02 and a time factor of 10.
Complex diffusion with a sigma of 0.02 and a time factor of 10.
|
P. Perona, J. Malik: "Scale-Space and Edge Detection Using Anisotropic Diffusion", IEEE Trans. Pattern Anal. Mach. Intell., 12(7), 1990. C. R. Vogel, M. E. Oman: "Iterative Methods for Total Variation Denoising", SIAM Journal on Scientific Computing, 17(1), 1996. M. J. Black, G. Sapiro, D. Marimont, D. Heeger: Robust anisotropic diffusion, IEEE Trans. on Image Processing, 7(3), 1998. G. Gilboa, N. A. Sochen, Y.Y. Zeevi, "Image Enhancement and Denoising by Complex Diffusion Processes", IEEE Trans. Pattern Anal. Mach. Intell. 26(8), 2004. Rui Bernardes, Cristina Maduro, Pedro Serranho, Aderito Araujo, Silvia Barbeiro, and Jose Cunha-Vaz: "Improved adaptive complex diffusion despeckling filter", Optics Express, 18(23), 24048-24059, 2010. | Denoise an image with Perona-Malik isotropic diffusion. Many proposed algorithms in the literature can be formulated such that they fit in the Perona-Malik framework. We implemented some of them: Perona-Malik diffusion, Diffusion with "Tuckey" edge stopping function, complex Diffusion by Gilboa et al., intensity senstive diffusion by Bernardes et al.
Implementation author:  Markus Mayer Markus Mayer |
| Anisotropic Diffusion (diffusionAnisotropic.m) |  Anisotropic diffusion with a Tuckey edge-stoping function, a sigma of 0.005 and a time factor of 4.
Anisotropic diffusion with a Tuckey edge-stoping function, a sigma of 0.005 and a time factor of 4.
|
Joachim Weickert: "Anisotropic Diffuion in Image Processing", ECMI Series, Teubner-Verlag, Stuttgart, Germany, 1998, available online. | Denoise an image with Perona-Malik isotropic diffusion. Anisotropic image diffusion as defined by Joachim Weickert. The implementation contains anisotropic diffusion with Perona-Malik and Tuckey edge stoping functions, as well as coherence enhancing diffusion.
Implementation author:  Markus Mayer Markus Mayer |
| Bayesian Estimation Denoising (bayesEstimateDenoise.m) | 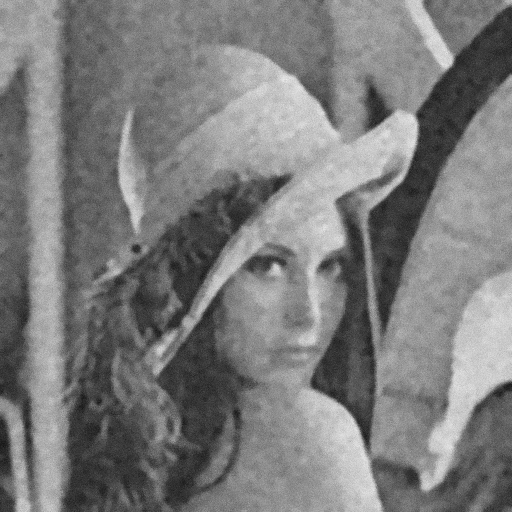 Bayesian estimation denoising with a spatial sigma of 3, a window size of 7x7, and a sigma-cut-off factor of 2.
Bayesian estimation denoising with a spatial sigma of 3, a window size of 7x7, and a sigma-cut-off factor of 2.
|
Alexander Wong, Akshaya Mishra, Kostadinka Bizheva and David A.Clausi: "General Bayesian estimation for speckle noise reduction in optical coherence tomography retinal imagery", Optics Express, April 2010, Vol. 18, No. 8, 8338--8352 | Denoise an image with Perona-Malik isotropic diffusion. A method that can be settled somewhere in between non-local means and the bilateral Filter. A pixel is replaced by a weighted average of random samples in its neighborhood. The samples have to fulfill a similarity criterion.
Implementation authors:  Markus Mayer and Markus Mayer and  Martin Kraus Martin Kraus |
| Wavelet Multiframe Denoising (waveletMultiFrame.zip) |  Wavelet multiframe denoising of a volume consisting of 4 "lena" frames with random Gaussian noise (standart deviation of 0.2). The dual-tree wavelet transformation, combined p-weight, a k-Parameter of 6 and a p-Parameter of 4 was utilized.
Wavelet multiframe denoising of a volume consisting of 4 "lena" frames with random Gaussian noise (standart deviation of 0.2). The dual-tree wavelet transformation, combined p-weight, a k-Parameter of 6 and a p-Parameter of 4 was utilized.
|
Markus A. Mayer, Anja Borsdorf, Martin Wagner, Joachim Hornegger, Christian Y. Mardin, and Ralf P. Tornow: "Wavelet denoising of multiframe optical coherence tomography data", Biomedical Optics Express, 2012 (accepted, to appear) | A denoising method based on wavelet decompositions. It works on multiple frame data, i.e. all images show the same content, but with varying noise. Read the paper for more details.
Implementation authors: Martin Wagner and  Markus Mayer Markus Mayer |
| Quantile Sparse Image (QuaSI) prior denoising ( | Franziska Schirrmacher, Thomas Köhler, Lennart Husvogt, James G. Fujimoto, Joachim Hornegger, Andreas Maier: QuaSI: Quantile Sparse Image Prior for Spatio-Temporal Denoising of Retinal OCT Data | A denoising algorithm based on the Quantile Sparse Image (QuaSI) prior to handle non-Gaussian noise. This method implements denoising in an energy minimization framework using a median filter regularization obtained from the QuaSI prior. It has been introduced for spatio-temporal noise reduction in optical coherence tomography (OCT) B-scans |
|---|
Evaluation Algorithms Matlab Code
The following algorithms and codes may help you to build up an evaluation for denoising algorithms. They are implemented in Matlab (Mathworks, Inc.).
| Method, Download | Reference | Description, Implementation Author |
|---|---|---|
| Image Noise Estimation (noiseest_matlab.zip) | S. M. Yang and S. C. Tai: "Fast and reliable image-noise estimation using a hybrid approach". Journal of Electronic Imaging 19(3), pp. 033007-1–15, 2010. dx.doi.org/10.1117/1.3476329 | A completely automated image noise estimation method. Image structure is excluded using a Sobel edge detector and an automatic thresholding. Noise is estimated on the remaining homogeneous parts by convolution with a Laplacian kernel. Optionally, the estimate can be refined iteratively. Implementation author:  Chris Schwemmer Chris Schwemmer |
Evaluation Data
The following data collections have been acquired in our lab or together with our collaborators. The paper in which they were used is referenced.
| Download, Reference | Image Examples | Description |
|---|---|---|
| Pigeye dataset Markus A. Mayer, Anja Borsdorf, Martin Wagner, Joachim Hornegger, Christian Y. Mardin, and Ralf P. Tornow: "Wavelet denoising of multiframe optical coherence tomography data", Biomedical Optics Express, 2012 (accepted, to appear) 1) pigeyeOriginal.zip (144 MB) 2) pigeyeRegistered.zip (152 MB) 3) pigeyeRaw.zip (350 MB) |  A single frame out of the database.
A single frame out of the database.
|
The pigeye data set, that we utilized in the journal paper on the wavelet multiframe denoising method. A description of the dataset can be found in the paper. There are 3 files for download:
1) pigeyeOrig: A .zip file containing intensity log scaled .tif files of each of the original frames in the pigeye data set. The numbering is the following: the first number depicts the acquisition position (1 to 35), the second the frame captured (1 to 13).
2) pigeyeReg: A .zip file containing intensity log scaled .tif files of each of the registered frames in the pigeye data set. The registration was performed as described in the paper. The numbering is the same as in pigeyeOrig.
3) pigeyeRaw: A .zip file containing the .vol files for each of the 35 acquisition positions, as exported from the Heidelberg Engineering Spectralis OCT. The intensities are linearly scaled and stored in 32 bit floating point numbers. Matlab code for opening this files can be found  here. here.
|
Impressum
Responsible for the content of this webpage:  Markus Mayer. There is no guarantee given that any of the codes available for download here are correcty implemented and/or free of bugs. Use the implementations at your own risk.
Markus Mayer. There is no guarantee given that any of the codes available for download here are correcty implemented and/or free of bugs. Use the implementations at your own risk.


 +49-9131-85-27775
+49-9131-85-27775
 +49-9131-85-27270
+49-9131-85-27270
