Contact

+49 9131 85 25247

+49 9131 85 27270
Address
Universität Erlangen-Nürnberg
Chair of Computer Science 5 (Pattern Recognition)
Martensstrasse 3
91058 Erlangen
Germany
Powered by

|
Limited Angle Tomography
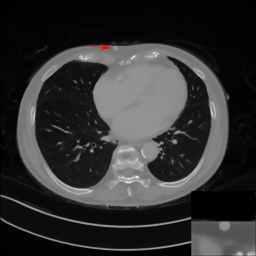
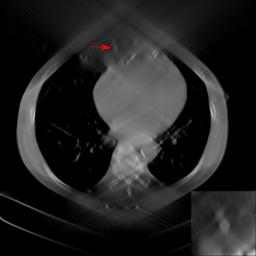
In computed tomography (CT), the X-ray source and the detector of a CT system need to rotate at least π plus a fan angle to get complete data for image reconstruction, which is called a short scan. However, in practical applications, the gantry rotation might be restricted by other system parts or external obstacles. In such cases, only limited angle data are acquired. Image reconstruction from data acquired in an insufficient angular range is called limited angle tomography. Due to missing data, artifacts occur in the reconstructed images. They cause boundary distortion, intensity leakage, and edge blurring as demonstrated in Fig. 1(b). Especially, a lot of streak artifacts occur along the missing angular ranges.
To improve image quality in limited angle tomography, we have investigated the following three methods: missing data interpolation/extrapolation using data consistency conditions  [1], iterative reconstruction with total variation regularization [1], iterative reconstruction with total variation regularization  [2], and machine learning including conventional machine learning [2], and machine learning including conventional machine learning  [3] and deep learning [3] and deep learning  [4]. [4].
Fig. 1(a). Custom phantom | Fig. 1(b). FBP reconstruction from 160-degree fan-beam sinogram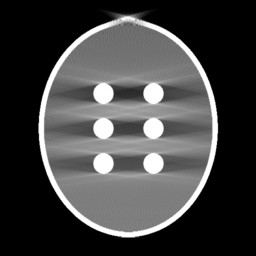 | Missing Data Restoration in Limited Angle Tomography based on Helgason-Ludwig Consistency Conditions
In computed tomography, there are many kinds of redundancy information, which are typically mathematically expressed as data consistency conditions. The Helgason-Ludwig consistency condition (HLCC) is the most well-known data consistency condition. One way to get HLCC is to use the Chebyshev Fourier transform (CFT). CFT can decompose a parallel-beam sinogram into different frequency components as demonstrated in Fig. 2.
HLCC can be used to restore missing data in limited angle tomography. Using CFT, we convert the missing data restoration problem into a regression problem and the Lasso regression is utilized. Due to severe ill-posedness, regression only recovers the low frequency components correctly. Bilateral filtering is utilized to retain the most prominent high frequency components. Afterwards, a fusion in the frequency domain utilizes the restored frequency components to fill the missing double wedge region. The proposed method is evaluated in a parallel-beam study on both numerical and clinical phantoms. The results show that our method is promising in streak reduction and intensity offset compensation in both noise-free and noisy situations.
Fig. 2(a). Restored sinograms using different orders | Fig. 2(b). Reconstructed images using different orders | Fig. 2(c). Fourier components of the reconstructed images using different orders | Scale-Space Anisotropic Total Variation for Limited Angle Tomography
Conventional Machine Learning for Limited Angle Tomography
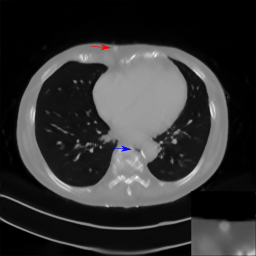
In this work, the application of traditional machine learning techniques, in the form of regression models based on conventional, "hand-crafted" features, to streak reduction in limited angle tomography is investigated. Specifically, linear regression (LR), multi-layer perceptron (MLP), and reduced-error pruning tree (REPTree) are investigated. When choosing the mean-variation-median (MVM), Laplacian, and Hessian features, REPTree learns streak artifacts best and reaches the smallest root-mean-square error (RMSE) of 29 HU for the Shepp-Logan phantom. Further experiments demonstrate that the MVM and Hessian features complement each other, whereas the Laplacian feature is redundant in the presence of MVM. In fan-beam, the SVDL features are also beneficial. Preliminary experiments on clinical data suggests that further investigation of clinical applications using REPTree may be worthwhile.
Fig. 4(a). Reference clinical image.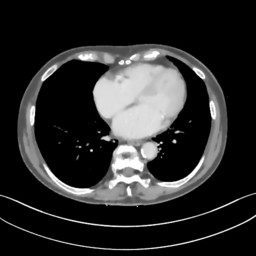 | Fig. 4(b). Image reconstructed from 160-degree fan-beam projection data.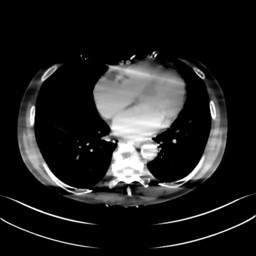 | Fig. 4(c). Image reconstructed by REPTree.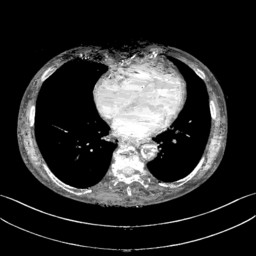 | Conventional Machine Learning Flowchart
Fig. 5. A fowchart summarizes our implementation of machine learning algorithms for limited angle tomography.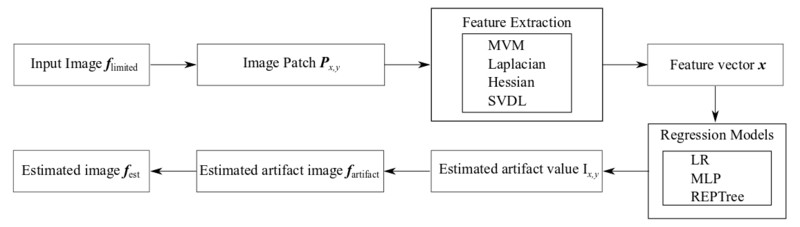 | Deep Learning for Limited Angle Tomography
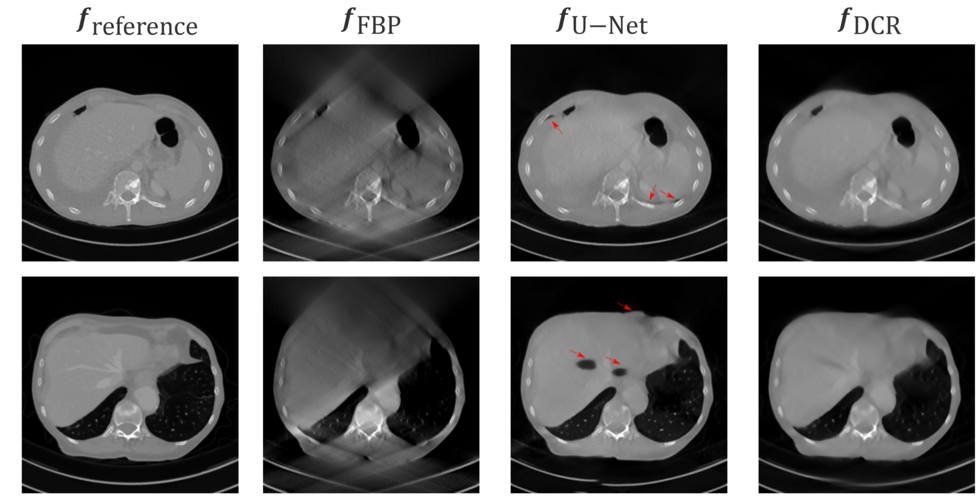
Recently, deep learning methods have been applied very successfully to many medical imaging problems including limited angle tomography. In our study, deep learning achieves the best performance compared with the above conventional methods. Even in a small angular range like 120°, deep learning can still obtain very good image quality. Fig. 6 displays the reconstruction results learnt by the popular neural network U-Net.
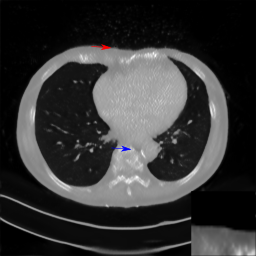
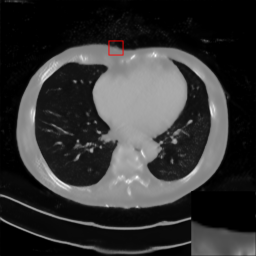
Although deep learning has achieved a lot of success, the robustness of neural networks for clinical applications is still a concern. It is reported that most neural networks are vulnerable to adversarial examples. Therefore, we aim to investigate whether some perturbations or noise will mislead a neural network to fail to detect an existing lesion. Our experiments demonstrate that the trained neural network, specifically the U-Net, is sensitive to Poisson noise. While the observed images appear artifact-free, anatomical structures may be located at wrong positions, e.g. the skin shifted by up to 1 cm. This kind of behavior can be reduced by retraining on data with simulated Poisson noise. However, we demonstrate that the retrained U-Net model is still susceptible to adversarial examples.
The modified U-Net for Limited Angle Tomography
Fig. 7. The modified U-Net architecture for artifact reduction in limited angle tomography with an example of 256×256 input images.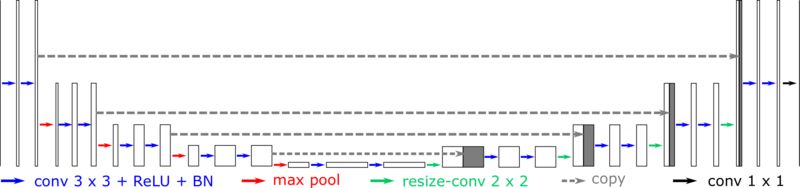 | Data Consistent Reconstruction with Deep Learning Prior
Robustness of deep learning methods for limited angle tomography is challenged by two major factors:
a) due to insufficient training data the network may not generalize well to unseen data;
b) deep learning methods are sensitive to noise.
Thus, generating reconstructed images directly from a neural network appears inadequate. We propose to constrain the reconstructed images to be consistent with the measured projection data, while the unmeasured information is complemented by learning based methods. For this purpose, a data consistent reconstruction (DCR) method is introduced:
First, a prior image is generated from an initial limited angle reconstruction via deep learning as a substitute for missing information.
Afterwards, a conventional iterative reconstruction algorithm is applied, integrating the data consistency in the measured angular range and the prior information in the missing angular range.
This ensures data integrity in the measured area, while inaccuracies incorporated by the deep learning prior lie only in areas where no information is acquired.
The proposed DCR method achieves significant image quality improvement: for 120-degree cone-beam limited angle tomography more than 10% RMSE reduction in noise-free case and more than 24% RMSE reduction in noisy case compared with a state-of-the-art U-Net based method.
|

 +49 9131 85 25247
+49 9131 85 25247
 +49 9131 85 27270
+49 9131 85 27270